
中学二年生の数学から、それまでに全くなかった新しい分野が登場します。
それが「証明」です。
それまでの数学は問題に対して計算を行い、答えを求めるものでしたが、証明では既にある答えに対して、なぜそうなるのかを文章で説明せねばなりません。
多くの生徒さんが証明に苦手意識を持ちますが、実は証明には大切な意味があります。今回は、特に三角形の合同に関する証明について、基礎からわかりやすく解説していきます。証明の考え方を身につければ、論理的思考力が養われ、日常生活でも役立つスキルが身につきます。では、さっそく証明の世界に踏み込んでいきましょう!
証明とは

証明とは、ある命題(主張)が正しいことを、既に知っている事実や定理を用いて論理的に説明することです。数学の証明では、「〜だから」「したがって」などの言葉を使って、段階的に理由を積み重ねていきます。
例えば、「この三角形は二等辺三角形である」という命題があったとします。これを証明するには、「二つの辺の長さが等しいこと」や「二つの角の大きさが等しいこと」などを示す必要がありますよね。
関連記事:数学の文字式が苦手な中学生必見!身近な例から、たった3ステップで文字式を完全攻略!
証明を苦手に感じる理由

多くの生徒さんが証明を苦手に感じる理由には、以下のようなものがあります:
- 抽象的な思考が必要:具体的な数字を扱う計算と違い、文字や図形を使って一般的な場合を考える必要があります。
- 論理的な文章力が求められる:自分の考えを筋道立てて文章にして説明する力が必要です。
- 何から始めればいいかわからない:証明の糸口をつかむのが難しいと感じる人も多いです。
- 正解が一つではない:同じ結論でも、証明の方法が複数ある場合があります。
関連記事:数学の成績を劇的にアップ!高校入試に勝つ、連立方程式マスターガイド
証明を通じて身につくもの

証明を学ぶことで、以下のような力が身につきます:
- 論理的思考力:物事を順序立てて考える力が養われます。
- 抽象的思考力:具体例だけでなく、一般的な法則を見出す力が身につきます。
- 表現力:自分の考えを正確に伝える力が向上します。
- 問題解決能力:複雑な問題を段階的に解決する力が身につきます。
これらの力は、数学だけでなく、他の教科や日常生活でも役立ちます。
証明の解き方を解説
ここでは、三角形の合同に関する証明を例に解説します。まず、三角形の合同条件について確認しましょう。
三角形の合同条件
- 3組の辺が、それぞれ等しいとき。
- 2組の辺とその間の角が、それぞれ等しいとき。
- 1組の辺とその両端の角が、それぞれ等しいとき。
では、上記を踏まえたうえで簡単な証明問題を見てみましょう。
関連記事:プロ家庭教師が教える中学数学のコツ!比例・反比例はこれで完全マスター!
証明の例題
問題
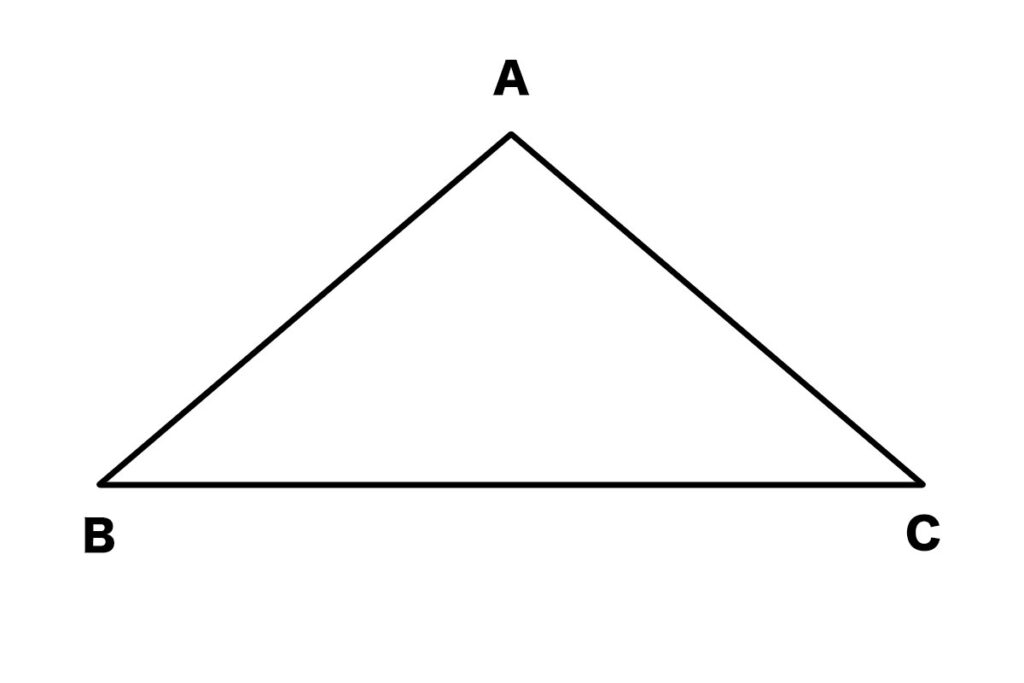
辺AB = 辺AC で、角B = 角C のとき、この三角形ABCが二等辺三角形であることを証明しましょう。
証明
- 分かっていること
・辺AB = 辺AC (与えられた条件)
・角B = 角C (与えられた条件)
・辺BCは両方の三角形で同じ - 考え方
二等辺三角形になるには、2つの辺が等しければOKです。
すでに辺AB = 辺ACと分かっているので、
これが本当に正しいか確認できれば証明完了です。 - 証明の手順
(1) 辺AB = 辺AC (与えられた条件から)
(2) 角B = 角C (与えられた条件から)
(3) 辺BCは共通 (同じ三角形の辺だから)
(4) これらの条件から、三角形の合同条件の
「2つの辺とその間の角がそれぞれ等しい」に当てはまります。
(5) よって、三角形ABCは二等辺三角形です。
証明問題を解く際のポイント
証明問題を解く際には以下のポイントを意識しましょう。
- 与えられた情報を整理する
- 何を示せばいいか確認する
- 知っている定理や性質を思い出す
- 順番に考えていく
- 各ステップの理由を明確に書く
具体的には以下のように実践していけるはずです。
- 与えられた情報を整理する
- 与えられた条件を図に書き込みましょう。
- 例:辺AB = 辺ACなら、両方に同じ印(例:|や◯)をつける。
- 何を示せばいいか確認する
- 証明の目標を忘れないようにペンでその箇所に線を引くようにしましょう。
- 例:「△ABCは二等辺三角形であることを示す」
- 使えそうな定理や公式を思い出す
- 教科書やノートを見返して、関連する内容をチェック。
- 例:三角形の合同条件、二等辺三角形の性質など
- 「もし〜なら」と仮定して考えてみる
- 結論から逆算して、どういう条件が必要か考えます。
- 例:「もし二等辺三角形なら、2つの辺が等しいはず」
- 小さなステップに分けて考える
- 一気に証明しようとせず、少しずつ進めます。
- 例:まず2つの三角形が合同かどうか確認し、 次に合同なら何が言えるか考える。
- 理由を「〜だから」の形で書く
- 各ステップの根拠を明確にします。
- 例:「2辺とその間の角が等しいから、合同」
- 分からないときは、似た問題を探す
- 教科書や問題集の例題を参考にしましょう。
- 解き方のパターンを見つけることが大切です。
- 証明が終わったら見直す
- 各ステップに飛躍がないか確認します。
- 結論に到達できているか、最終チェック。
このように、与えられた条件を使って、順序立てて考えていくことが証明の基本です。難しく感じるかもしれませんが、練習を重ねるうちに上達していきますよ。最初は時間がかかっても大丈夫です。根気強く取り組んでいきましょう!
関連記事:【数学】変数?定数?一次関数(y=ax+b)について徹底解説!
証明の練習問題
問題1
下の図のような三角形ABCと三角形DEFがあります。
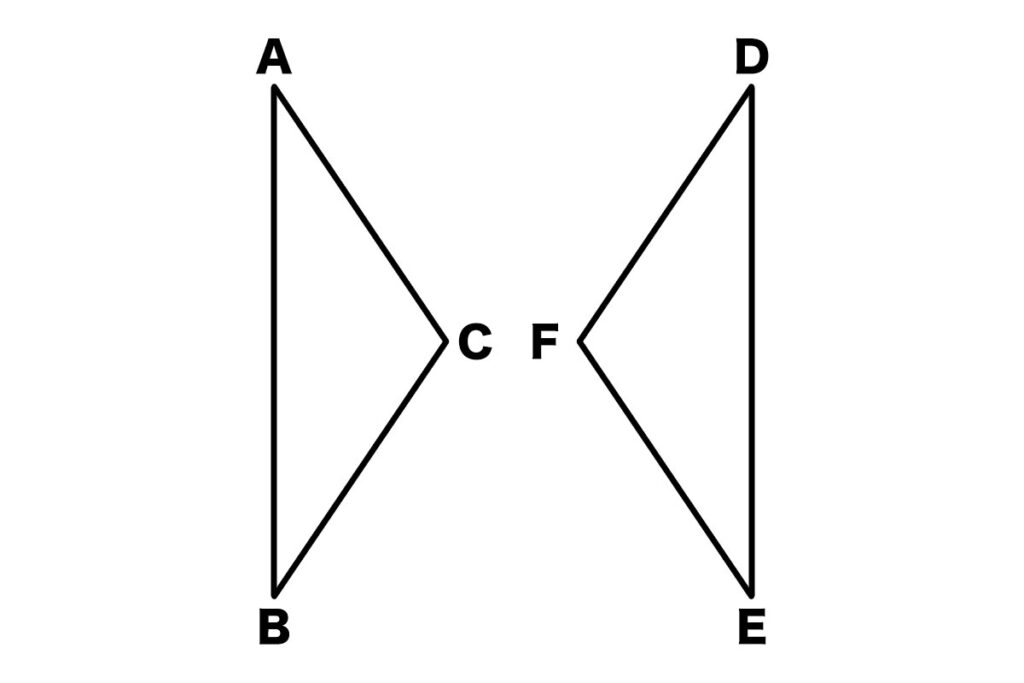
次の条件が成り立つとき、証明の( )に適切な語句を入れて、三角形ABCと三角形DEFが合同であることを証明しなさい。
条件
・AB = DE
・AC = DF
・角BAC = 角EDF
証明
三角形ABCと三角形DEFにおいて、
(1) AB = DE, AC = DF ( )
(2) 角BAC = 角EDF ( )
(3) したがって、【 】ため、
三角形ABC ≡ 三角形DEF (合同)
ヒント
(1)と(2)の( )には、どのような条件が与えられているかを書きましょう。
(3)の【 】には、使用した合同条件を書きましょう。
答えと解説
証明
三角形ABCと三角形DEFにおいて、
(1) AB = DE, AC = DF (仮定より/与えられた条件から)
(2) 角BAC = 角EDF (仮定より/与えられた条件から)
(3) したがって、【2組の辺とその間の角が,それぞれ等しい】ため、
三角形ABC ≡ 三角形DEF (合同)
解説
(1) (2) 「仮定より」は、問題で与えられた条件を指す際の一般的な表現です。「仮定より」と「与えられた条件から」はどちらも正解です。問題文の条件を参照していることを示す表現として、どちらも適切です。
(3) この問題では、「2組の辺とその間の角が、それぞれ等しい」の条件を使って三角形の合同を証明しています。
(1)で2つの辺が等しいこと、(2)でその間の角が等しいことが分かります。
これらの条件が揃っているので、(3)で「2組の辺とその間の角が、それぞれ等しい」を用いて合同であると結論づけることができます。
関連記事:数学で点数アップの重要単元「方程式」のマスター方法!
問題2
次の図のような三角形ABCがあります。
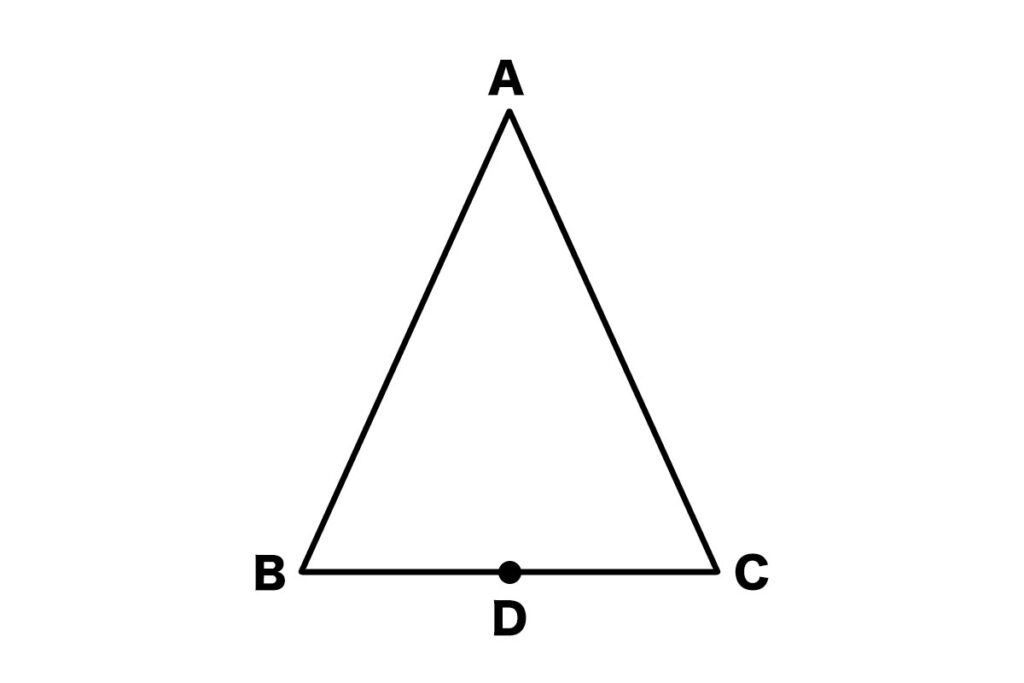
問題
以下の条件のとき、AD ⊥ BC(ADはBCに垂直)であることを証明しなさい。
条件
・AB = AC(辺ABと辺ACの長さが等しい)
・点Dは辺BCの中点
ヒント
二等辺三角形の性質を思い出しましょう。
三角形の合同条件を考えてみましょう。
点Dは辺BCの中点であることを使いましょう。
答えと解説
証明
(1) 仮定より、AB = AC
(2) したがって、三角形ABCは二等辺三角形である
(3) 二等辺三角形の性質より、∠BAC = ∠BCA
(4) 点Dは辺BCの中点なので、BD = DC
(5) AD = AD(共通)
(6) ∠BAD = ∠CAD((3)より、∠BAC の二等分線がAD)
(7) (4), (5), (6)より、△ABD ≡ △ACD(「2組の辺とその間の角が、それぞれ等しい」の合同条件)
(8) 合同な三角形の対応する角は等しいので、∠ADB = ∠ADC
(9) ∠ADB + ∠ADC = 180°(直線上の角の和)
(10) よって、∠ADB = ∠ADC = 90°
(11) したがって、AD ⊥ BC
解説
この問題では、二等辺三角形の性質と三角形の合同条件を組み合わせて証明を行います。
まず、与えられた条件から二等辺三角形の性質を導き出し、それを基に三角形の合同を示します。
合同な三角形の性質を使って、最終的に垂直であることを証明しています。
この証明では、論理的な段階を追って結論を導き出す過程が重要です。
関連記事:数学嫌いが直る!苦手科目1位の数学で点数アップさせる唯一の方法
問題3
次の図のような四角形ABCDがあります。
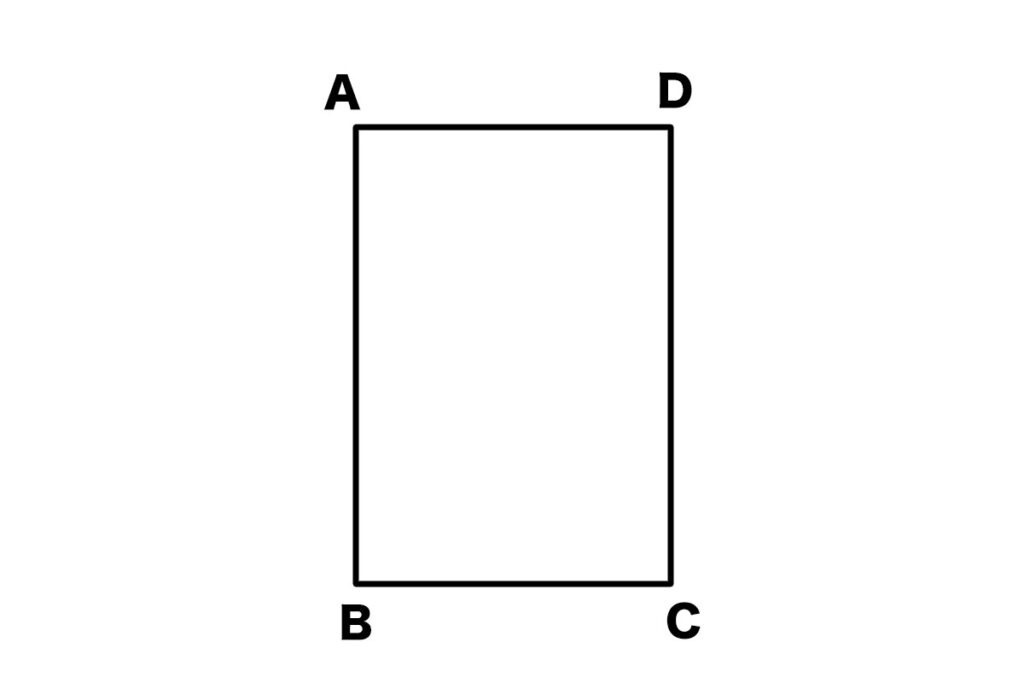
AB = AD、CB = CD のとき、角ABC = 角ADC であることを証明しなさい。
ヒント
四角形を2つの三角形に分けて考えてみましょう。
それぞれの三角形について、何が言えるでしょうか。
答えと解説
証明
(1) 仮定より、AB = AD、CB = CD
(2) AC(対角線)は共通
(3) したがって、三角形ABC と三角形ADC において、
3つの辺がそれぞれ等しい
(4) よって、三辺の長さが等しいので、
三角形ABC ≡ 三角形ADC (合同)
(5) 合同な図形の対応する角は等しいので、
角ABC = 角ADC
解説
この問題では、四角形を対角線ACで2つの三角形に分け、それらの合同を示すことで結論を導いています。
(1)と(2)で3組の辺が等しいことを確認し、(3)と(4)で3組の辺が、それぞれ等しいことを用いて三角形の合同を示しています。
最後に(5)で、合同な図形の性質を用いて、求めたい角が等しいことを結論づけています。
関連記事:小学生算数の苦手克服!「速さ」をマスターして中学受験も乗り越えよう!
まとめ

証明は、最初は難しく感じるかもしれませんが、基本的な考え方や手順を押さえれば、徐々に理解できるようになります。大切なのは、与えられた条件を整理し、何を示したいのかを明確にすることです。そして、既知の定理や性質を用いて、段階的に論理を組み立てていくのです。
証明を学ぶことで、論理的思考力や問題解決能力が身につきます。これらのスキルは、数学だけでなく、他の教科や日常生活でも役立ちます。例えば、レポートを書くときや、自分の意見を説明するときにも活かせるでしょう。
最初は難しく感じても、諦めずに少しずつ練習を重ねていけば、必ず上達します。わからないところがあれば、先生や友達に質問するのも良いでしょう。証明を通じて、数学の奥深さや面白さを発見できることを願っています。がんばってください!













